Your Error propagation example problems images are available. Error propagation example problems are a topic that is being searched for and liked by netizens now. You can Download the Error propagation example problems files here. Find and Download all royalty-free images.
If you’re looking for error propagation example problems pictures information connected with to the error propagation example problems interest, you have come to the right site. Our site always provides you with suggestions for viewing the maximum quality video and picture content, please kindly surf and locate more informative video content and images that fit your interests.
Error Propagation Example Problems. Propagation of errors A number of measured quantities may be involved in the final calculation of an experiment. Therefore they will only be unitless if the original quantity is. In addition a key aspect of the method is a shift of computational expense to a precomputation phase. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3.
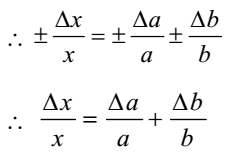Propagation Of Errors In Addition Subtraction Multiplication And Division From thefactfactor.com
Find the sum of the lengths of the two rods with the limit of errors. 1 f is a function in several variables x i each with their own uncertainty Δ x i. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. The possible errors are adequately covered in the discussion above. Basic formula for propagation of errors The formulas derived in this tutorial for each different mathematical operation are based on taking the partial derivative of a function with respect to each variable that has uncertainty. 1 𝑅 1 𝑅1 1 𝑅2 1 𝑅3 Where 𝑅1𝑅1𝑅1 𝑅2𝑅2𝑅2 and 𝑅3𝑅3𝑅3 are the absolute uncertainties for those resistors.
Basic formula for propagation of errors The formulas derived in this tutorial for each different mathematical operation are based on taking the partial derivative of a function with respect to each variable that has uncertainty.
Power in an electric circuit. Fractional Uncertainties Chapter 2 and Propagation of Errors Chapter 3 2 Propagation of Errors Introduction to Propagation of Errors In determining a physical quantity it is only very rarely that we make a direct experimental measurement on the quantity itself. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. We know that in addition the errors get added up. Top-down approach consists of estimating the. Then q x D 2020 p 0012 032 206.
Source: youtube.com
Absolute errors will have the same units as the orig-inal quantity2 so a time measured in seconds will have an uncertainty measured in seconds etc. The parallel combination of three resistors R 1 R 2 and R 3 is written as. Propagation of error considerations. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. Then r 0.
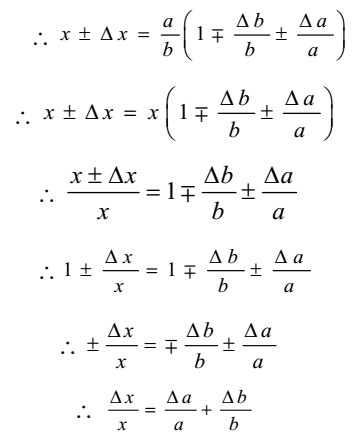Source: thefactfactor.com
The response matrix method has been a useful solution method for radiation transport problems for decades. 1 f is a function in several variables x i each with their own uncertainty Δ x i. Propagation of errors A number of measured quantities may be involved in the final calculation of an experiment. There is no shortage of papers online that attempt to explain how backpropagation works but few that include an example with actual numbers. In addition a key aspect of the method is a shift of computational expense to a precomputation phase.
Source: thefactfactor.com
Ben Buckner LS PE CP Ben Buckner is an educator author and seminar presenter with Surveyors Educational Seminars and was a contributing author for the magazine. This video was create. Different types of instruments might have been used for taking readings. In addition a key aspect of the method is a shift of computational expense to a precomputation phase. Finally a note on units.
Source: brainkart.com
Top-down approach consists of estimating the. For example dont use the Simple Rule for Products and Ratios for a power function such as z x 2 since the two x s in the formula would be correlated with each other. This lesson discusses how to predict the manner in which random errors accumulate when calculations are performed with measured values. Now suppose you want to know the uncertainty in the radius. For example suppose the radius of a circle is measured to be r 6 cm but the exact value of the radius if it could be measured with infinite precision is 6.
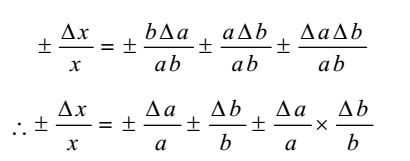Source: thefactfactor.com
Therefore they will only be unitless if the original quantity is. The result is a general equation for the propagation of uncertainty that is given as Eqn. Top-down approach consists of estimating the. 1 f is a function in several variables x i each with their own uncertainty Δ x i. Much more often it is the.
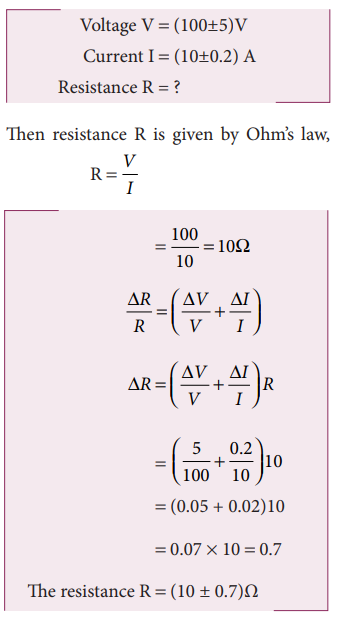Source: brainkart.com
Absolute errors will have the same units as the orig-inal quantity2 so a time measured in seconds will have an uncertainty measured in seconds etc. For example suppose the radius of a circle is measured to be r 6 cm but the exact value of the radius if it could be measured with infinite precision is 6. Much more often it is the. Where the three uncertainties are independent and random. Propagation of Errors Basic Rules.
Source: brainkart.com
Top-down approach consists of estimating the. It can be extended to both fixed source and eigenvalue problems. We know that in addition the errors get added up. Propagating Errors for Experiment 1 3 4 e g GR ρ π Formula for density. Absolute errors will have the same units as the orig-inal quantity2 so a time measured in seconds will have an uncertainty measured in seconds etc.
Source: id.pinterest.com
Find the sum of the lengths of the two rods with the limit of errors. Much more often it is the. Measurement Process Characterization 25. We know that in addition the errors get added up. Suppose two measured quantities x and y have uncertainties Dx and Dy determined by procedures described in previous sections.
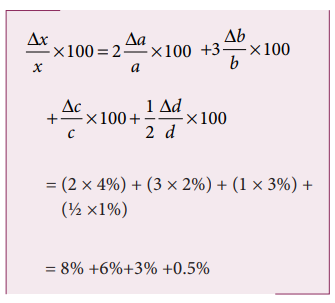Source: brainkart.com
Then q x D 2020 p 0012 032 206. Measurement Process Characterization 25. Ben Buckner LS PE CP Ben Buckner is an educator author and seminar presenter with Surveyors Educational Seminars and was a contributing author for the magazine. Top-down approach consists of estimating the. For example if you measure the diameter of a sphere to be d 100 008 cm then the fractional uncertainty in dis 8.
Source: brainkart.com
A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. The method is desirable for many reasons. 1 f is a function in several variables x i each with their own uncertainty Δ x i. In conclusion the experiment met the objective of the volume lab. We would report x Dx and y DyFrom the measured quantities a new quantity z is calculated from.
Source: brainkart.com
In conclusion the experiment met the objective of the volume lab. Propagation of Errors Basic Rules. Researchers like it because they have proofs that back-propagation will work. For example dont use the Simple Rule for Products and Ratios for a power function such as z x 2 since the two x s in the formula would be correlated with each other. Measurement Process Characterization 25.
Source: youtube.com
Although this seems like a daunting task the problem is solvable and it has been solved but the proof will not be given here. Yet its success does not preclude other methods from optimizing neurons. 1 𝑅 1 𝑅1 1 𝑅2 1 𝑅3 Where 𝑅1𝑅1𝑅1 𝑅2𝑅2𝑅2 and 𝑅3𝑅3𝑅3 are the absolute uncertainties for those resistors. Let D yz 102 p 2 103. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3.
Source: brainkart.com
Ben Buckner LS PE CP Ben Buckner is an educator author and seminar presenter with Surveyors Educational Seminars and was a contributing author for the magazine. 1 𝑅 1 𝑅1 1 𝑅2 1 𝑅3 Where 𝑅1𝑅1𝑅1 𝑅2𝑅2𝑅2 and 𝑅3𝑅3𝑅3 are the absolute uncertainties for those resistors. Fractional Uncertainties Chapter 2 and Propagation of Errors Chapter 3 2 Propagation of Errors Introduction to Propagation of Errors In determining a physical quantity it is only very rarely that we make a direct experimental measurement on the quantity itself. Neural Networks rely upon back-propagation by gradient descent to set the weights of neurons connections. Suppose you measure three numbers as follows.
Source: pinterest.com
Backpropagation is a common method for training a neural network. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. Different types of instruments might have been used for taking readings. Now suppose you want to know the uncertainty in the radius. Top-down approach consists of estimating the.
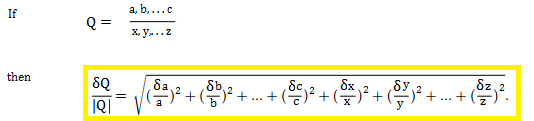Source: statisticshowto.com
Use step-by-step propagation to find the quantity q xy z with its uncertainty. Basic formula for propagation of errors The formulas derived in this tutorial for each different mathematical operation are based on taking the partial derivative of a function with respect to each variable that has uncertainty. This post is my attempt to explain how it works with a concrete example that folks can compare their own calculations to in order to ensure they. Example Problem 37d of text Atd t k th fll i tA student makes the following measurement. Fractional Uncertainties Chapter 2 and Propagation of Errors Chapter 3 2 Propagation of Errors Introduction to Propagation of Errors In determining a physical quantity it is only very rarely that we make a direct experimental measurement on the quantity itself.
Source: thefactfactor.com
Propagation of Errors 3 u If x and y are correlated define sxy as. Use step-by-step propagation to find the quantity q xy z with its uncertainty. Backpropagation is a common method for training a neural network. Researchers like it because they have proofs that back-propagation will work. Measurement Process Characterization 25.
Source: youtube.com
Propagation of Errors 3 u If x and y are correlated define sxy as. Absolute errors will have the same units as the orig-inal quantity2 so a time measured in seconds will have an uncertainty measured in seconds etc. In addition a key aspect of the method is a shift of computational expense to a precomputation phase. Suppose you measure three numbers as follows. Measurement Process Characterization 25.
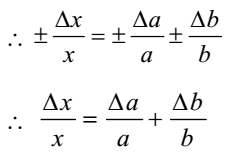Source: thefactfactor.com
Example Problem 37d of text Atd t k th fll i tA student makes the following measurement. A 5 1 cm b 18 2 cm c 12 1 cm t 30 05 s m 18 1 gram Compute the quantity mbt with its uncertainties and percentage uncertainties mb t t f b b f m m f f t f δ δ δ δ 05 cm-gs 3 18 18 2 3. The parallel combination of three resistors R 1 R 2 and R 3 is written as. Backpropagation is a common method for training a neural network. Much more often it is the.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title error propagation example problems by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
