Your Hypotenuse leg theorem examples images are available in this site. Hypotenuse leg theorem examples are a topic that is being searched for and liked by netizens today. You can Download the Hypotenuse leg theorem examples files here. Get all free photos.
If you’re searching for hypotenuse leg theorem examples pictures information connected with to the hypotenuse leg theorem examples topic, you have pay a visit to the ideal blog. Our website frequently gives you suggestions for seeking the maximum quality video and picture content, please kindly search and locate more informative video articles and graphics that match your interests.
Hypotenuse Leg Theorem Examples. Because they both have a right angle. This theorem is really a derivation of the Side Angle Side Postulate just as the HA Theorem is a derivation of the Angle Side Angle Postulate. This principle is known as Hypotenuse-Leg theorem. Solution EXAMPLE 2 Use the Pythagorean theorem to find the missing length.
Hypotenuse Leg Theorem Easily Explained W 15 Examples From calcworkshop.com
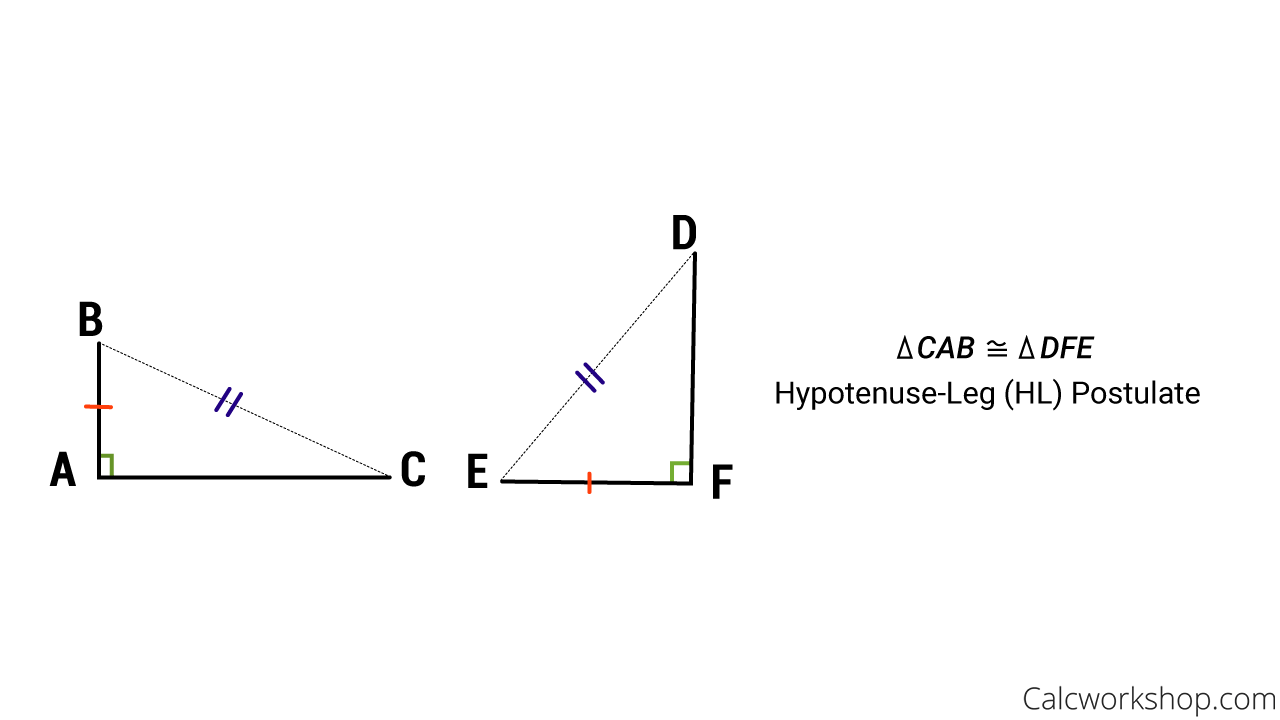
Substitute values into the formula remember C is the hypotenuse. The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the legs or eqa2b2c2 eq where c is the hypotenuse and a and b are the legs of the. Hypotenuse Theorem Example Using the image above if segment AB is congruent to segment FE and segment BC is congruent to segment ED then triangle CAB is congruent to triangle DFE. In this lesson we will look at several different types of examples of applying this theorem. Use the Pythagorean theorem to determine the length of X. This principle is known as Hypotenuse-Leg theorem.
Identify the legs and the hypotenuse of the right triangle.
There is one pair of congruent legs. Solution EXAMPLE 3 A right triangle has legs of length 9 and 13. The triangles have congruent hypotenuses. Identify the legs and the hypotenuse of the right triangle. For example in the right triangle below the hypotenuse is side c and the legs are sides a and b. By the hypotenuse formula we know.
Source: youtube.com
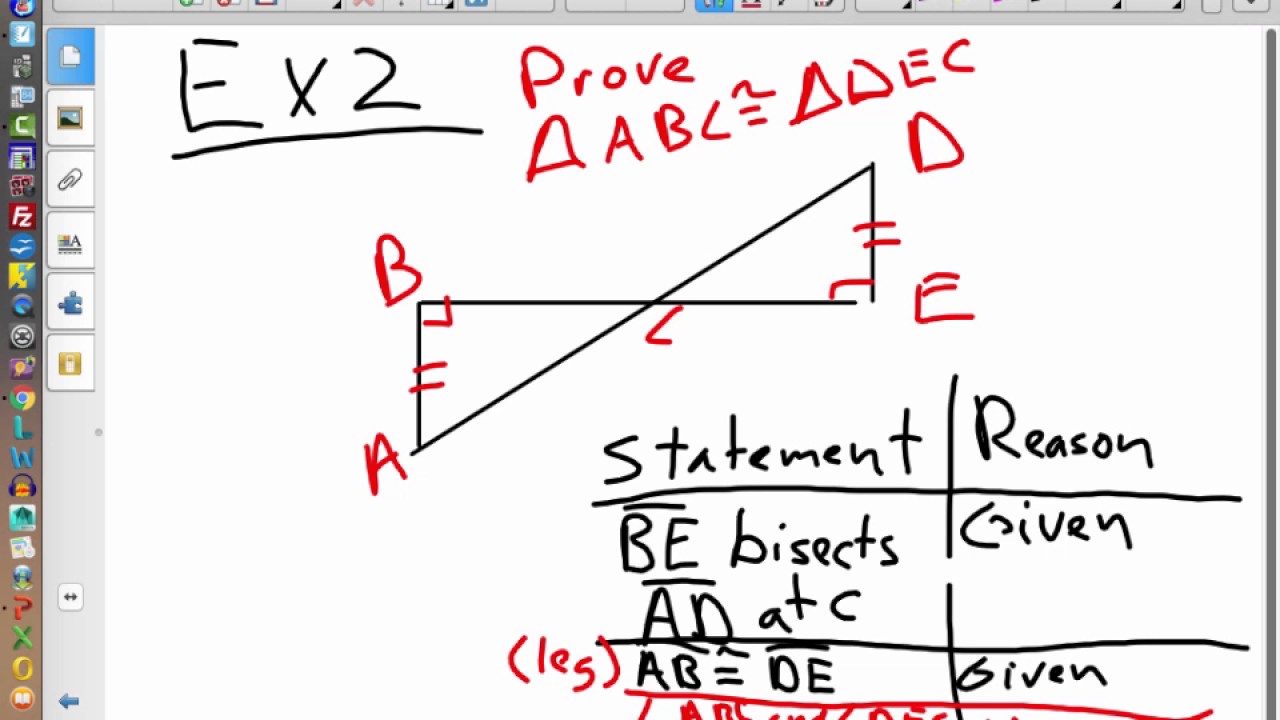
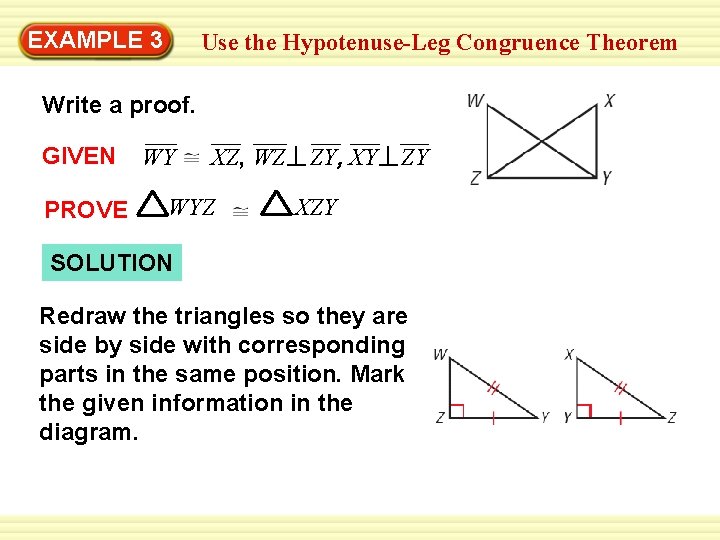
Example 1 If PR QS prove that PQR and PRS are congruent Solution Triangle PQR and PRS are right triangles because they both have a 90-degree angle at point R. 1 Answer Camilleon Apr 25 2018 The Hypotenuse-Leg Theorem states that if the leg and hypotenuse of one triangle is equal to the leg and hypotenuse of another triangle then they are congruent. Hypotenuse leg theorem exampleswhat is hypotenuse leg theoremwhat is hl theorem examples. Example 2 If FB DB BA BC FB AE and DB CE show that AE CE. Right triangles get their name from one identifying property.
Source: study.com
Definitions Right Triangles CPCTC SAS Postulate HL Theorem Proving the HL Theorem. Example 2 If FB DB BA BC FB AE and DB CE show that AE CE. Substitute values into the formula remember C is the hypotenuse. View Hypotenuse_Leg_Congruenceppt from MATH 11 at Pangasinan State University - Urdaneta City. 1 Answer Camilleon Apr 25 2018 The Hypotenuse-Leg Theorem states that if the leg and hypotenuse of one triangle is equal to the leg and hypotenuse of another triangle then they are congruent.
Source: tutors.com
I Triangle ABC and triangle CDE are right triangles. Given base 3cm and perpendicular 4cm. Identifying Property of Right Triangles. EXAMPLE 1 Determine the length of X using the Pythagorean theorem. Observe the following isosceles triangle ABC in which side AB AC and AD is perpendicular to BC.
Source: youtube.com
Given base 3cm and perpendicular 4cm. Hypotenuse Theorem Example Using the image above if segment AB is congruent to segment FE and segment BC is congruent to segment ED then triangle CAB is congruent to triangle DFE. 54 Hypotenuse-Leg HL Congruence Theorem Objective. Other Triangle Congruence Postulates and Theorems 1. 1 1 HL2 HL3 Not congruent4 Not congruent 5 HL6 HL7 ZY ZR or XZ SZ 8 CD RQ9 VW UE10.
Source: ck12.org
Substitute values into the formula remember C is the hypotenuse. It must of course be a triangle meaning it is a three-sided polygon. Rational Expressions Partial Portion Decomposition Example. Substitute values into the formula remember C is the hypotenuse. Let us solve some examples based on the hypotenuse concept.
Source: cuemath.com
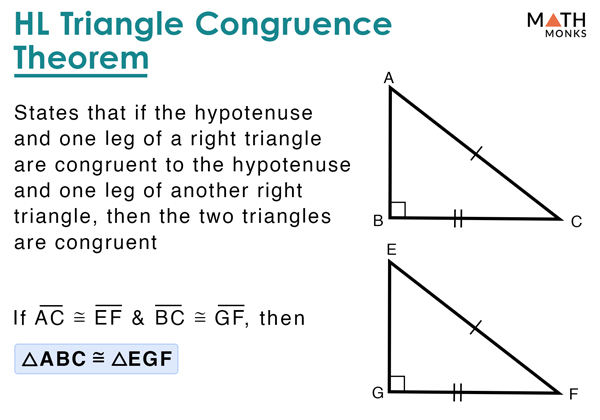
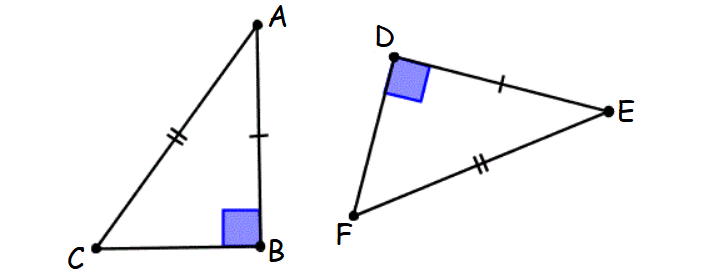
If the base and perpendicular of a right-angled triangle are 3cm and 4cm respectively find the hypotenuse. Right triangles get their name from one identifying property. I AC CE Leg ii BC CD Leg Hence the two triangles ABC and CDE are congruent by Leg-Leg theorem. This formula allows us to find the length of the hypotenuse if we know the length of the two legs. ABC XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.
Source: youtube.com
The hypotenuse is 26. Right triangles get their name from one identifying property. Also any of the other two sides the base or the perpendicular side can be easily calculated for the given value of the hypotenuse. There are two right triangles. View Hypotenuse_Leg_Congruenceppt from MATH 11 at Pangasinan State University - Urdaneta City.
Source: mathematicalway.com
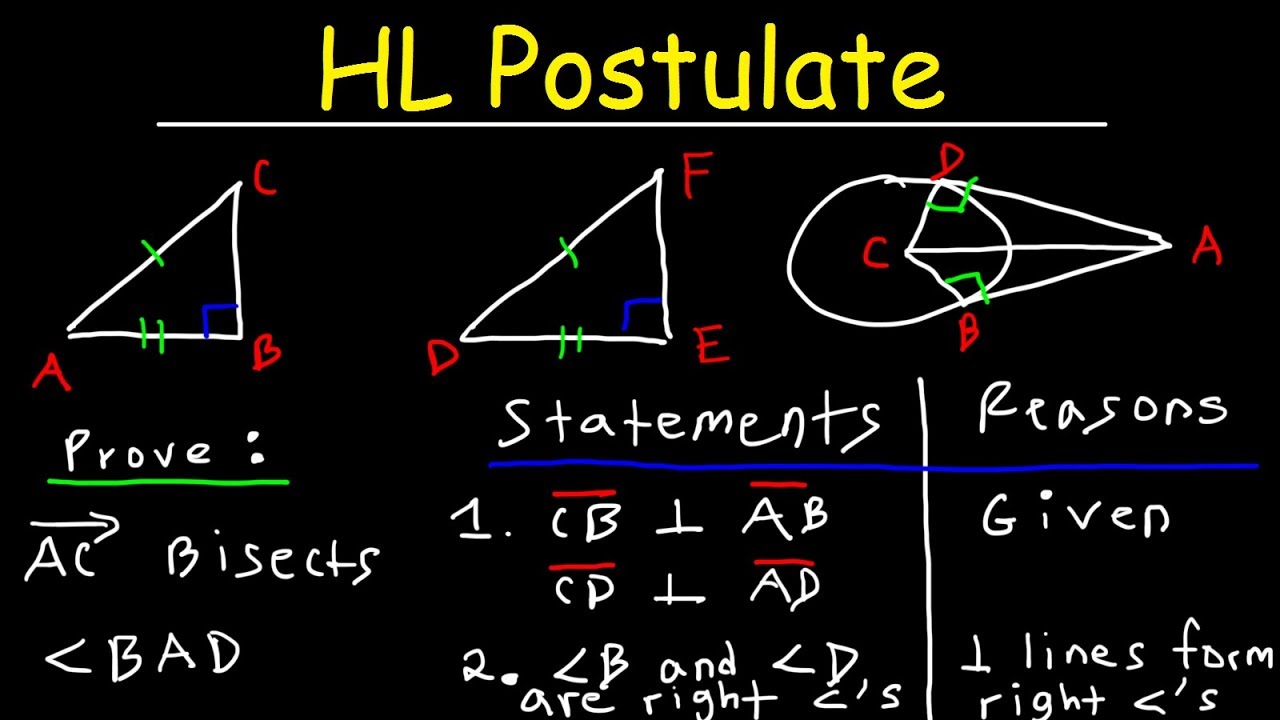
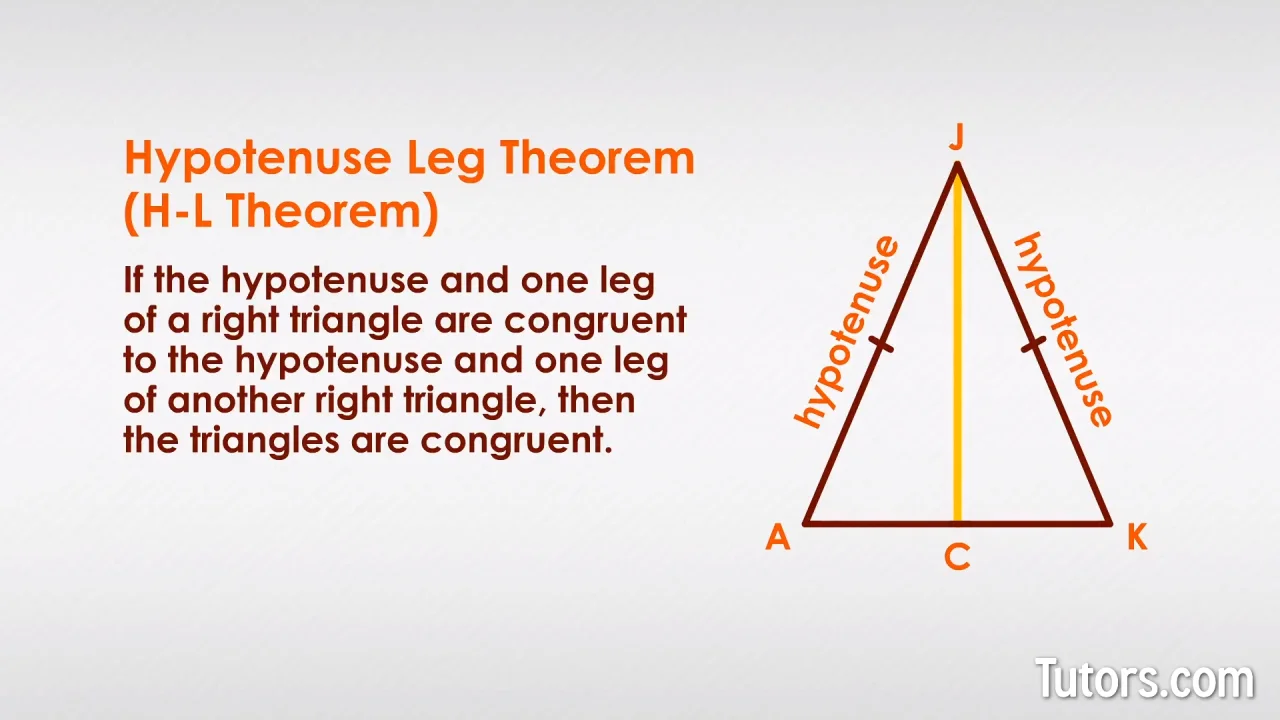
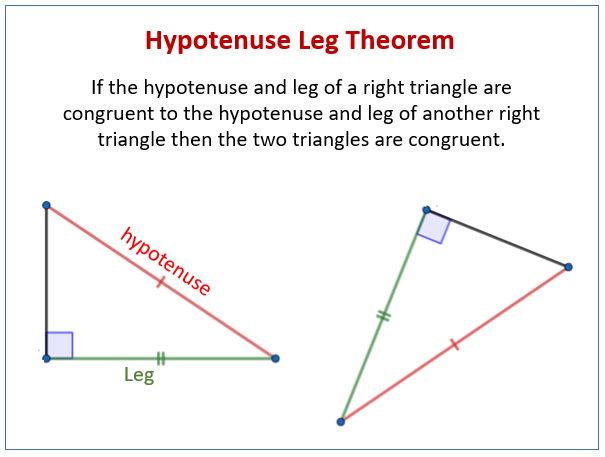
The hypotenuse leg HL theorem states that two right triangles are congruent if the hypotenuse one leg of a right triangle are congruent to the hypotenuseleg of another right triangle. Now at first glance it looks like we are going against our cardinal rule of not allowing side-side-anglewhich spells the bad word ie the reverse of SSA. Hypotenuse Leg In right triangles if two legs are congruent and if the two hypotenuses are congruent then the triangles are congruent. View Hypotenuse_Leg_Congruenceppt from MATH 11 at Pangasinan State University - Urdaneta City. Use the Pythagorean theorem to determine the length of X.
Source: youtube.com
The triangles have congruent hypotenuses. 1 1 HL2 HL3 Not congruent4 Not congruent 5 HL6 HL7 ZY ZR or XZ SZ 8 CD RQ9 VW UE10. Definitions Right Triangles CPCTC SAS Postulate HL Theorem Proving the HL Theorem. If so state the triangle congruence and name the postulate that is used. By the hypotenuse formula we know.
Source: youtube.com
The legs have length 24 and X are the legs. Hypotenuse leg theorem exampleswhat is hypotenuse leg theoremwhat is hl theorem examples. Hypotenuse 2 Base 2 Perpendicular 2 6 2 8 2 36 64 100. PQ PS Hypotenuse PR PR Common side Therefore by Hypotenuse Leg HL theorem PQR PR. The proof of the hypotenuse leg theorem shows how a given set of right triangles are congruent if the corresponding lengths of their hypotenuse and one leg are equal.
Source: mathmonks.com
The triangles have congruent hypotenuses. The Pythagorean theorem is a way of relating the leg lengths of a right triangle to the length of the hypotenuse which is the side opposite the right angle. Hypotenuse Leg In right triangles if two legs are congruent and if the two hypotenuses are congruent then the triangles are congruent. It cannot have two interior right angles because then it would not be a triangle. 1 1 HL2 HL3 Not congruent4 Not congruent 5 HL6 HL7 ZY ZR or XZ SZ 8 CD RQ9 VW UE10.
Source: calcworkshop.com
If so state the triangle congruence and name the postulate that is used. View Hypotenuse_Leg_Congruenceppt from MATH 11 at Pangasinan State University - Urdaneta City. Hypotenuse 2 Base 2 Perpendicular 2 6 2 8 2 36 64 100. By the hypotenuse formula we know. Hypotenuse Theorem Example Using the image above if segment AB is congruent to segment FE and segment BC is congruent to segment ED then triangle CAB is congruent to triangle DFE.
Source: tutors.com
Here ABC is an isosceles triangle AB AC and AD is perpendicular to BC. Hypotenuse leg theorem exampleswhat is hypotenuse leg theoremwhat is hl theorem examples. Because they both have a right angle. The following formula is helpful to calculate the measure of the hypotenuse. Hypotenuse 2 Base 2 Perpendicular 2 6 2 8 2 36 64 100.
Source: cuemath.com
EXAMPLE 1 Determine the length of X using the Pythagorean theorem. Solution EXAMPLE 3 A right triangle has legs of length 9 and 13. What is the length of its hypotenuse. Even though it is written in these terms it can be used to find any of the side as long as you know the lengths of the other two sides. It cannot have two interior right angles because then it would not be a triangle.
Source: cuemath.com
This formula allows us to find the length of the hypotenuse if we know the length of the two legs. PQ PS Hypotenuse PR PR Common side Therefore by Hypotenuse Leg HL theorem PQR PR. Hypotenuse 100 10 inches. Also any of the other two sides the base or the perpendicular side can be easily calculated for the given value of the hypotenuse. 1 1 HL2 HL3 Not congruent4 Not congruent 5 HL6 HL7 ZY ZR or XZ SZ 8 CD RQ9 VW UE10.
Source: slidetodoc.com
Even though it is written in these terms it can be used to find any of the side as long as you know the lengths of the other two sides. Also any of the other two sides the base or the perpendicular side can be easily calculated for the given value of the hypotenuse. Now at first glance it looks like we are going against our cardinal rule of not allowing side-side-anglewhich spells the bad word ie the reverse of SSA. There are two right triangles. This theorem is really a derivation of the Side Angle Side Postulate just as the HA Theorem is a derivation of the Angle Side Angle Postulate.
Source: onlinemathlearning.com
Here ABC is an isosceles triangle AB AC and AD is perpendicular to BC. Use the Pythagorean theorem to determine the length of X. The hypotenuse leg HL theorem states that two right triangles are congruent if the hypotenuse one leg of a right triangle are congruent to the hypotenuseleg of another right triangle. Hypotenuse Leg In right triangles if two legs are congruent and if the two hypotenuses are congruent then the triangles are congruent. Answers to Hypotenuse Leg Practice ID.
Source: onlinemath4all.com
EXAMPLE 1 Determine the length of X using the Pythagorean theorem. The triangles have congruent hypotenuses. I Triangle ABC and triangle CDE are right triangles. If the base and perpendicular of a right-angled triangle are 3cm and 4cm respectively find the hypotenuse. The Pythagorean theorem is a way of relating the leg lengths of a right triangle to the length of the hypotenuse which is the side opposite the right angle.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title hypotenuse leg theorem examples by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
