Your Rolles theorem examples images are available. Rolles theorem examples are a topic that is being searched for and liked by netizens today. You can Get the Rolles theorem examples files here. Download all royalty-free vectors.
If you’re searching for rolles theorem examples images information connected with to the rolles theorem examples interest, you have visit the right site. Our website always gives you hints for seeing the highest quality video and picture content, please kindly surf and locate more enlightening video articles and images that fit your interests.
Rolles Theorem Examples. In general one can understand mean as the average of the given values. In order to utilize the Mean Value Theorem in examples we need first to understand another called Rolles Theorem. Lets take a look at a quick example that uses Rolles Theorem. But in the case of integrals the process of finding the mean value of two different.
7 1 Derivatives With Mean Value Theorem And Rolle S Theorem K12 Libretexts From k12.libretexts.org
32 Rolles Theorem and the Mean Value Theorem Rolles Theorem Let f be continuous on the closed interval a b and differentiable on the open interval a b. Movement of a particle If s ft is a smooth function describing the position of an object in a straight line. It is a special case of and in fact is equivalent to the mean value theorem which in turn is an essential ingredient in the proof of the fundamental theorem of calculus. Lets look at an example to see this in action. Show that f x 1 x x 2 satisfies the hypothesis of Rolles Theorem on 0 4 and find all values of c in 0 4 that satisfy the conclusion of the theorem. They are formulated.
FREE Cuemath material for JEECBSE ICSE for excellent results.
F is differentiable its derivative is 2 x 1. Show that f x 1 x x 2 satisfies the hypothesis of Rolles Theorem on 0 4 and find all values of c in 0 4 that satisfy the conclusion of the theorem. If not explain why not. Rolles Theorem was first proven in 1691 just seven years after the first paper involving Calculus was published. If the object is in the same position at times t a and t b then fa fb and by Rolles theorem there must be a time c in between when vc. Now f1 f3 0 and thus function f satisfies all the three conditions of Rolles theorem.
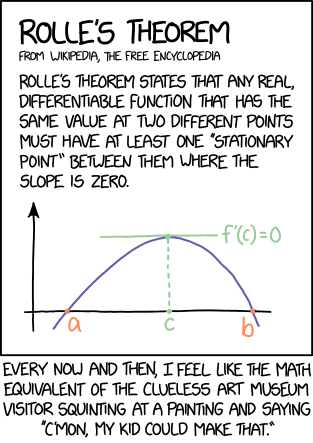Source: explainxkcd.com
In order to utilize the Mean Value Theorem in examples we need first to understand another called Rolles Theorem. Therefore f x is continuous on 2 3 and differentiable on 2 3. At the same time Lagranges mean value theorem is the mean value theorem itself or the first mean value theorem. In other words we can say that at every point of the interval the continuous curve passes through the same value of y at x-axis twice and has a unique tangent line. Suppose we are asked to determine whether Rolles theorem can be applied to fxx4-2 x2 on the closed interval -22.
Source: youtube.com
April 17 2020. Let f x x2 x. We seek a c in ab with fc 0. Movement of a particle If s ft is a smooth function describing the position of an object in a straight line. But in the case of integrals the process of finding the mean value of two different.
Source: slideplayer.com
While in the mean value theorem the minimum possibility of points giving the same slope equal to the secant of endpoints is discussed we explore the tangents of slope zero of functions in. 32 Rolles Theorem and the Mean Value Theorem Rolles Theorem Let f be continuous on the closed interval a b and differentiable on the open interval a b. In order to utilize the Mean Value Theorem in examples we need first to understand another called Rolles Theorem. Based on out previous work f is continuous on its domain which includes 0 4. 1 f x is defined and continuous on 0 2 2 f x is not differentiable on 0 2.
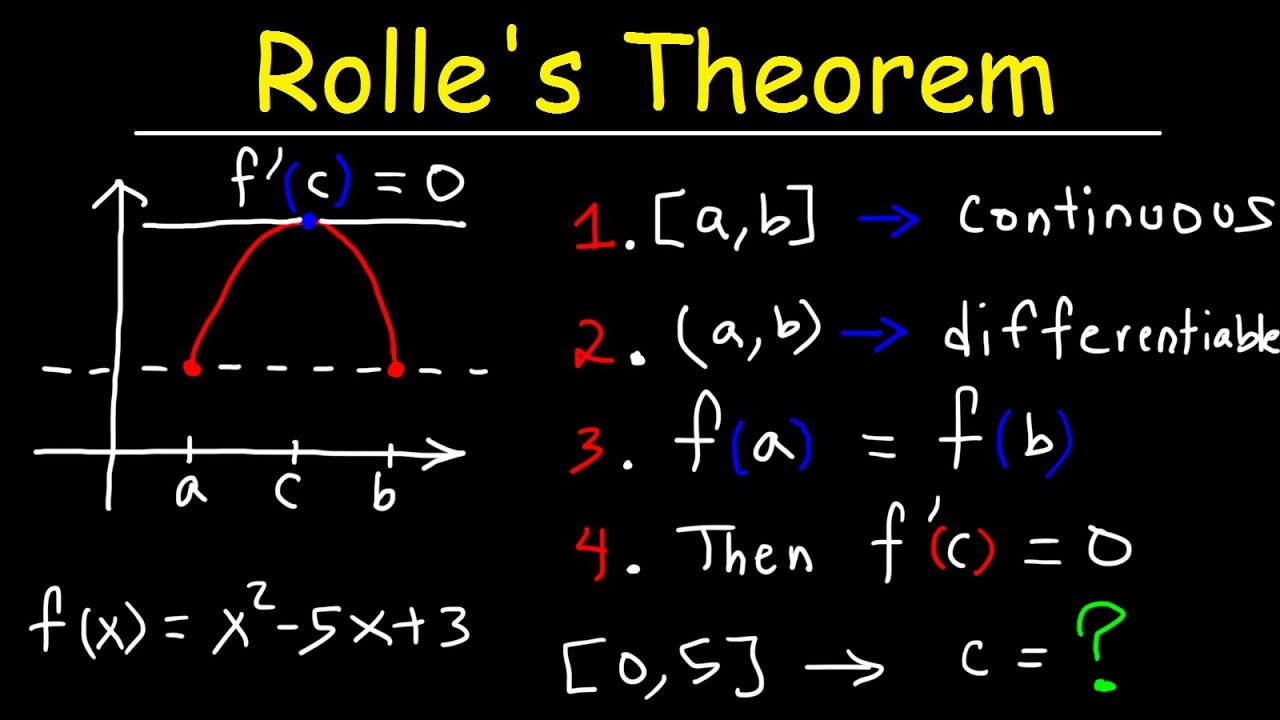Source: youtube.com
Rolles Theorem is a particular case of the mean value theorem which satisfies certain conditions. Therefore f x is continuous on 2 3 and differentiable on 2 3. From basic Algebra principles we know that since fleft x right is a 5 th degree polynomial it will have five roots. If f a f b 0 then there is at least one number c in a b such that fc. April 17 2020.
Source: slidetodoc.com
Since a polynomial function is everywhere differentiable and so continuous also. Based on out previous work f is continuous on its domain which includes 0 4. But in the case of integrals the process of finding the mean value of two different. Suppose we are asked to determine whether Rolles theorem can be applied to fxx4-2 x2 on the closed interval -22. Logarithmic function is continuous and differentiable in its domain.
Source: k12.libretexts.org
Let f x x2 x. Logarithmic function is continuous and differentiable in its domain. From basic Algebra principles we know that since fleft x right is a 5 th degree polynomial it will have five roots. This is explained by the fact that the 3textrd condition is not satisfied since fleft 0 right ne fleft 1 right Figure 5. Examples on Rolles Theorem and Lagranges.
Source: pdfprof.com
But in the case of integrals the process of finding the mean value of two different. They are formulated. Since a polynomial function is everywhere differentiable and so continuous also. Example 1 Show that fleft x right 4x5 x3 7x - 2 has exactly one real root. We discuss Rolles Theorem with two examples in this video math tutorial by Marios Math Tutoring021 What is Rolles Theorem.
Source: teachoo.com
32 Rolles Theorem and the Mean Value Theorem Rolles Theorem Let f be continuous on the closed interval a b and differentiable on the open interval a b. If not explain why not. In terms of our car example Rolles theorem says that if a moving car begins and ends at the same place then somewhere during this journey it must reverse direction since. This is explained by the fact that the 3textrd condition is not satisfied since fleft 0 right ne fleft 1 right Figure 5. Examples 83 Rolles Theorem and the Mean Value Theorem 1.
Source: slidetodoc.com
Let f x x2 x. If f x be a real valued function that satisfies the following three conditions. That is we wish to show that f has a horizontal tangent somewhere between a and b. This video contains plenty of examples. Show that f x 1 x x 2 satisfies the hypothesis of Rolles Theorem on 0 4 and find all values of c in 0 4 that satisfy the conclusion of the theorem.
Source: analyzemath.com
In other words we can say that at every point of the interval the continuous curve passes through the same value of y at x-axis twice and has a unique tangent line. Lets look at an example to see this in action. This calculus video tutorial explains the concept behind Rolles Theorem and the Mean Value Theorem For Derivatives. Rolles Theorem like the Theorem on Local Extrema ends with fc 0. Show that f x 1 x x 2 satisfies the hypothesis of Rolles Theorem on 0 4 and find all values of c in 0 4 that satisfy the conclusion of the theorem.
Source: analyzemath.com
In calculus the theorem says that if a differentiable function achieves equal values at two different points then it must possess at least one fixed point somewhere between them that is a position where the first derivative ie the slope of the. 1 f x is defined and continuous on 0 2 2 f x is not differentiable on 0 2. 32 Rolles Theorem and the Mean Value Theorem Rolles Theorem Let f be continuous on the closed interval a b and differentiable on the open interval a b. The proof of Rolles Theorem is a matter of examining cases and applying the Theorem on Local Extrema. If the object is in the same position at times t a and t b then fa fb and by Rolles theorem there must be a time c in between when vc.
Source: chegg.com
F is a polynomial function therefore is continuous on the interval 1 3 and is also differentiable on the interval 1 3. The Mean Value Theorem states that the rate of change at some point in a domain is equal to the average rate of change of that domain. In order to utilize the Mean Value Theorem in examples we need first to understand another called Rolles Theorem. If f a f b 0 then there is at least one number c in a b such that fc. From basic Algebra principles we know that since fleft x right is a 5 th degree polynomial it will have five roots.
Source: youtube.com
They are formulated. Find the two x-intercepts of the function f and show that fx 0 at some point between the. - Definition337 Example 1 Us. Rolles Theorem was first proven in 1691 just seven years after the first paper involving Calculus was published. If not explain why not.
Source: youtube.com
Examples 83 Rolles Theorem and the Mean Value Theorem 1. In general one can understand mean as the average of the given values. F is differentiable its derivative is 2 x 1. The mean value theorem has the utmost importance in differential and integral calculusRolles theorem is a special case of the mean value theorem. Example 1 Show that fleft x right 4x5 x3 7x - 2 has exactly one real root.
Source: unacademy.com
If not explain why not. Find the two x-intercepts of the function f and show that fx 0 at some point between the. 1 f x is defined and continuous on 0 2 2 f x is not differentiable on 0 2. It is a special case of and in fact is equivalent to the mean value theorem which in turn is an essential ingredient in the proof of the fundamental theorem of calculus. Rolles Theorem is a particular case of the mean value theorem which satisfies certain conditions.
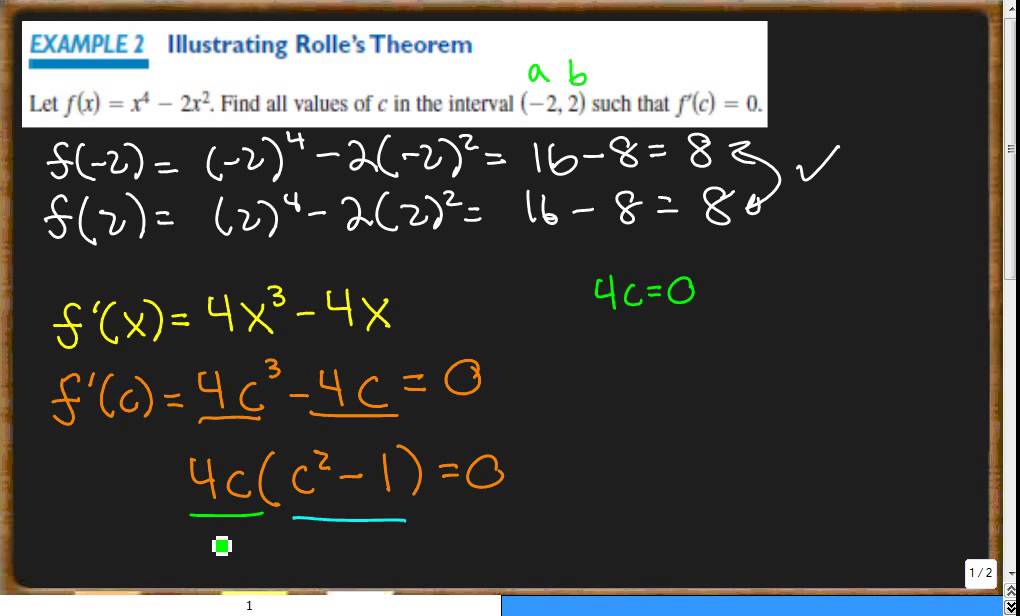Source: youtube.com
Verify Rolles theorem for the function fx x 2 - 4 x 3 on the interval 1 3 and then find the values of x c such that f c 0. Lets take a look at a quick example that uses Rolles Theorem. Since a polynomial function is everywhere differentiable and so continuous also. If not explain why not. If the object is in the same position at times t a and t b then fa fb and by Rolles theorem there must be a time c in between when vc.
Source: analyzemath.com
Logarithmic function is continuous and differentiable in its domain. Examples on Rolles Theorem and Lagranges. The mean value theorem has the utmost importance in differential and integral calculusRolles theorem is a special case of the mean value theorem. Therefore f x is continuous on 2 3 and differentiable on 2 3. In modern mathematics the proof of Rolles theorem is based on two other theorems the Weierstrass extreme value theorem and Fermats theorem.
Source: teachoo.com
In other words we can say that at every point of the interval the continuous curve passes through the same value of y at x-axis twice and has a unique tangent line. And if so find all values of c in the interval that. Examples On Rolles Theorem And Lagranges Theorem in Applications of Derivatives with concepts examples and solutions. In terms of our car example Rolles theorem says that if a moving car begins and ends at the same place then somewhere during this journey it must reverse direction since. But in the case of integrals the process of finding the mean value of two different.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title rolles theorem examples by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
